神经网络编程入门

　　本文主要内容包括： (1) 介绍神经网络基本原理，(2) AForge.NET实现前向神经网络的方法，(3) Matlab实现前向神经网络的方法 。

 

第0节、引例 

       本文以Fisher的Iris数据集作为神经网络程序的测试数据集。Iris数据集可以在http://en.wikipedia.org/wiki/Iris_flower_data_set  找到。这里简要介绍一下Iris数据集：

有一批Iris花，已知这批Iris花可分为3个品种，现需要对其进行分类。不同品种的Iris花的花萼长度、花萼宽度、花瓣长度、花瓣宽度会有差异。我们现有一批已知品种的Iris花的花萼长度、花萼宽度、花瓣长度、花瓣宽度的数据。

　　一种解决方法是用已有的数据训练一个神经网络用作分类器。

第一节、神经网络基本原理 

1. 人工神经元( Artificial Neuron )模型 

       人工神经元是神经网络的基本元素，其原理可以用下图表示：

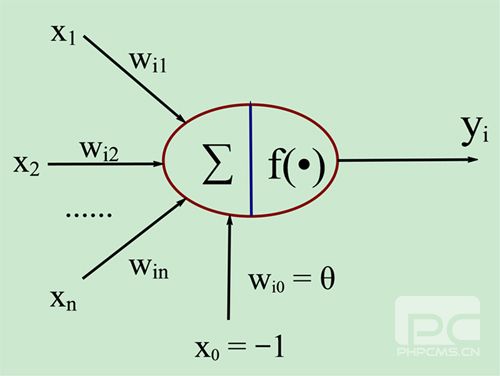
图1. 人工神经元模型

 

       图中x1~xn是从其他神经元传来的输入信号，wij表示表示从神经元j到神经元i的连接权值，θ表示一个阈值 ( threshold )，或称为偏置( bias )。则神经元i的输出与输入的关系表示为：

 

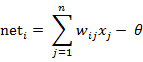
　　图中 yi表示神经元i的输出，函数f称为激活函数 ( Activation Function )或转移函数 ( Transfer Function ) ，net称为净激活(net activation)。若将阈值看成是神经元i的一个输入x0的权重wi0，则上面的式子可以简化为：

 

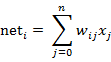
　　若用X表示输入向量，用W表示权重向量，即：

X = [ x0 , x1 , x2 , ....... , xn ]

 

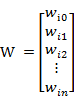
　　则神经元的输出可以表示为向量相乘的形式：

 

 

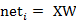
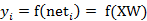
       若神经元的净激活net为正，称该神经元处于激活状态或兴奋状态(fire)，若净激活net为负，则称神经元处于抑制状态。

       图1中的这种“阈值加权和”的神经元模型称为M-P模型 ( McCulloch-Pitts Model )，也称为神经网络的一个处理单元( PE, Processing Element )。

 

2. 常用激活函数 

       激活函数的选择是构建神经网络过程中的重要环节，下面简要介绍常用的激活函数。

(1) 线性函数 ( Liner Function )

 

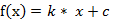
(2) 斜面函数 ( Ramp Function )

 

(3) 阈值函数 ( Threshold Function )

 

 

 

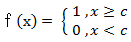
       以上3个激活函数都属于线性函数，下面介绍两个常用的非线性激活函数。

(4) S形函数 ( Sigmoid Function )

　　该函数的导函数：

(5) 双极S形函数 

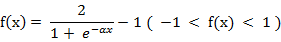
　　该函数的导函数：

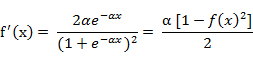
　　S形函数与双极S形函数的图像如下：

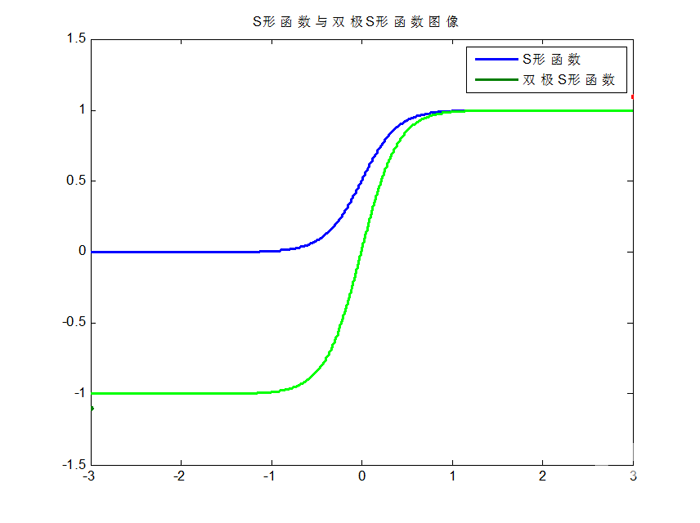
图3. S形函数与双极S形函数图像

　　双极S形函数与S形函数主要区别在于函数的值域，双极S形函数值域是(-1,1)，而S形函数值域是(0,1)。

　　由于S形函数与双极S形函数都是可导的(导函数是连续函数)，因此适合用在BP神经网络中。（BP算法要求激活函数可导）

 

3. 神经网络模型 

       神经网络是由大量的神经元互联而构成的网络。根据网络中神经元的互联方式，常见网络结构主要可以分为下面３类：

(1) 前馈神经网络　(　Feedforward Neural Networks )

       前馈网络也称前向网络。这种网络只在训练过程会有反馈信号，而在分类过程中数据只能向前传送，直到到达输出层，层间没有向后的反馈信号，因此被称为前馈网络。感知机( perceptron)与BP神经网络就属于前馈网络。

       图4 中是一个3层的前馈神经网络，其中第一层是输入单元，第二层称为隐含层，第三层称为输出层（输入单元不是神经元，因此图中有2层神经元）。

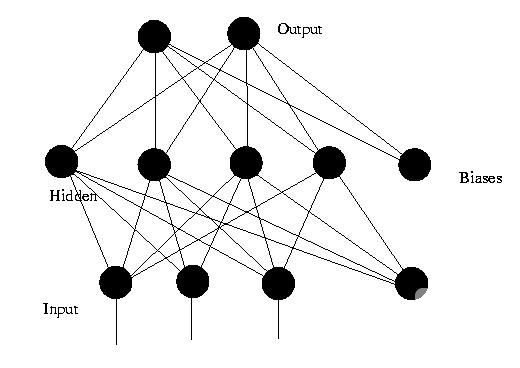
图4. 前馈神经网络

 

　　对于一个3层的前馈神经网络N，若用X表示网络的输入向量，W1~W3表示网络各层的连接权向量，F1~F3表示神经网络3层的激活函数。

　　那么神经网络的第一层神经元的输出为：

O1 = F1( XW1 )

　　第二层的输出为：

O2 = F2 ( F1( XW1 ) W2 )

　　输出层的输出为：

O3 = F3( F2 ( F1( XW1 ) W2 ) W3 )

       若激活函数F1~F3都选用线性函数，那么神经网络的输出O3将是输入X的线性函数。因此，若要做高次函数的逼近就应该选用适当的非线性函数作为激活函数。

(2) 反馈神经网络　(　Feedback Neural Networks )

       反馈型神经网络是一种从输出到输入具有反馈连接的神经网络，其结构比前馈网络要复杂得多。典型的反馈型神经网络有：Elman网络和Hopfield网络。

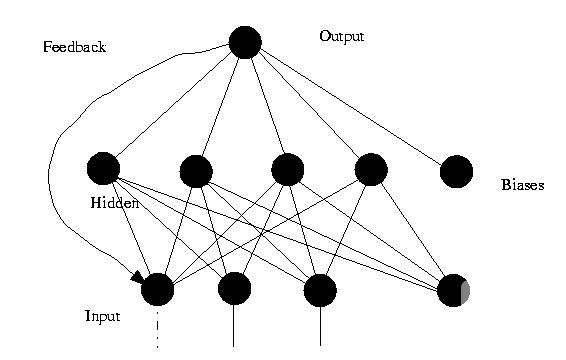
图5. 反馈神经网络

 

(3) 自组织网络 ( SOM ,Self-Organizing Neural Networks )

       自组织神经网络是一种无导师学习网络。它通过自动寻找样本中的内在规律和本质属性，自组织、自适应地改变网络参数与结构。

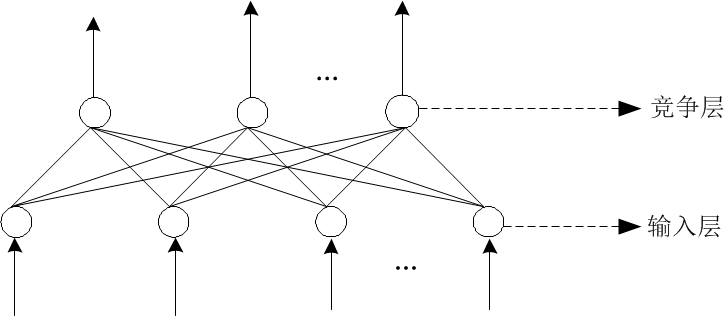
图6. 自组织网络

 

4. 神经网络工作方式 

       神经网络运作过程分为学习和工作两种状态。

(1)神经网络的学习状态 

       网络的学习主要是指使用学习算法来调整神经元间的联接权，使得网络输出更符合实际。学习算法分为有导师学习( Supervised Learning )与无导师学习( Unsupervised Learning )两类。

       有导师学习算法将一组训练集 ( training set )送入网络，根据网络的实际输出与期望输出间的差别来调整连接权。有导师学习算法的主要步骤包括：

1）  从样本集合中取一个样本（Ai，Bi）；

2）  计算网络的实际输出O；

3）  求D=Bi-O；

4）  根据D调整权矩阵W；

5） 对每个样本重复上述过程，直到对整个样本集来说，误差不超过规定范围。

　　BP算法就是一种出色的有导师学习算法。

       无导师学习抽取样本集合中蕴含的统计特性，并以神经元之间的联接权的形式存于网络中。

       Hebb学习律是一种经典的无导师学习算法。

(2) 神经网络的工作状态 

       神经元间的连接权不变，神经网络作为分类器、预测器等使用。

　　下面简要介绍一下Hebb学习率与Delta学习规则 。

(3) 无导师学习算法：Hebb学习率 

　　Hebb算法核心思想是，当两个神经元同时处于激发状态时两者间的连接权会被加强，否则被减弱。 

       为了理解Hebb算法，有必要简单介绍一下条件反射实验。巴甫洛夫的条件反射实验：每次给狗喂食前都先响铃，时间一长，狗就会将铃声和食物联系起来。以后如果响铃但是不给食物，狗也会流口水。

图7. 巴甫洛夫的条件反射实验

 

　　受该实验的启发，Hebb的理论认为在同一时间被激发的神经元间的联系会被强化。比如，铃声响时一个神经元被激发，在同一时间食物的出现会激发附近的另一个神经元，那么这两个神经元间的联系就会强化，从而记住这两个事物之间存在着联系。相反，如果两个神经元总是不能同步激发，那么它们间的联系将会越来越弱。

　　Hebb学习律可表示为：

       其中wij表示神经元j到神经元i的连接权，yi与yj为两个神经元的输出，a是表示学习速度的常数。若yi与yj同时被激活，即yi与yj同时为正，那么Wij将增大。若yi被激活，而yj处于抑制状态，即yi为正yj为负，那么Wij将变小。

(4) 有导师学习算法：Delta学习规则

　　Delta学习规则是一种简单的有导师学习算法，该算法根据神经元的实际输出与期望输出差别来调整连接权，其数学表示如下：

 

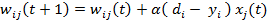
       其中Wij表示神经元j到神经元i的连接权，di是神经元i的期望输出，yi是神经元i的实际输出，xj表示神经元j状态，若神经元j处于激活态则xj为1，若处于抑制状态则xj为0或－1（根据激活函数而定）。a是表示学习速度的常数。假设xi为1，若di比yi大，那么Wij将增大，若di比yi小，那么Wij将变小。

       Delta规则简单讲来就是：若神经元实际输出比期望输出大，则减小所有输入为正的连接的权重，增大所有输入为负的连接的权重。反之，若神经元实际输出比期望输出小，则增大所有输入为正的连接的权重，减小所有输入为负的连接的权重。这个增大或减小的幅度就根据上面的式子来计算。

(5)有导师学习算法：BP算法 

　　采用BP学习算法的前馈型神经网络通常被称为BP网络。

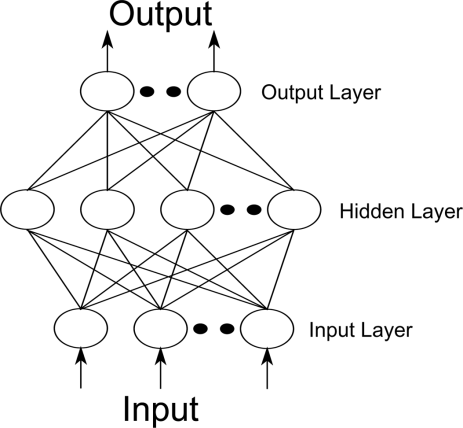
图8. 三层BP神经网络结构

 

　　BP网络具有很强的非线性映射能力，一个3层BP神经网络能够实现对任意非线性函数进行逼近（根据Kolrnogorov定理）。一个典型的3层BP神经网络模型如图7所示。

　　BP网络的学习算法占篇幅较大，我打算在下一篇文章中介绍。

 

第二节、神经网络实现 

 

1. 数据预处理 

       在训练神经网络前一般需要对数据进行预处理，一种重要的预处理手段是归一化处理。下面简要介绍归一化处理的原理与方法。

(1) 什么是归一化？ 

数据归一化，就是将数据映射到[0,1]或[-1,1]区间或更小的区间，比如(0.1,0.9) 。

(2) 为什么要归一化处理？ 

<1>输入数据的单位不一样，有些数据的范围可能特别大，导致的结果是神经网络收敛慢、训练时间长。

<2>数据范围大的输入在模式分类中的作用可能会偏大，而数据范围小的输入作用就可能会偏小。

<3>由于神经网络输出层的激活函数的值域是有限制的，因此需要将网络训练的目标数据映射到激活函数的值域。例如神经网络的输出层若采用S形激活函数，由于S形函数的值域限制在(0,1)，也就是说神经网络的输出只能限制在(0,1)，所以训练数据的输出就要归一化到[0,1]区间。

<4>S形激活函数在(0,1)区间以外区域很平缓，区分度太小。例如S形函数f(X)在参数a=1时，f(100)与f(5)只相差0.0067。

(3) 归一化算法 

　　一种简单而快速的归一化算法是线性转换算法。线性转换算法常见有两种形式：

       <1>

y = ( x - min )/( max - min )

　　其中min为x的最小值，max为x的最大值，输入向量为x，归一化后的输出向量为y 。上式将数据归一化到 [ 0 , 1 ]区间，当激活函数采用S形函数时（值域为(0,1)）时这条式子适用。

       <2>

y = 2 * ( x - min ) / ( max - min ) - 1

       这条公式将数据归一化到 [ -1 , 1 ] 区间。当激活函数采用双极S形函数（值域为(-1,1)）时这条式子适用。

(4) Matlab数据归一化处理函数 

　　Matlab中归一化处理数据可以采用premnmx ， postmnmx ， tramnmx 这3个函数。

<1> premnmx

语法：[pn,minp,maxp,tn,mint,maxt] = premnmx(p,t)

参数：

pn： p矩阵按行归一化后的矩阵

minp，maxp：p矩阵每一行的最小值，最大值

tn：t矩阵按行归一化后的矩阵

mint，maxt：t矩阵每一行的最小值，最大值

作用：将矩阵p，t归一化到[-1,1] ，主要用于归一化处理训练数据集。

<2> tramnmx

语法：[pn] = tramnmx(p,minp,maxp)

参数：

minp，maxp：premnmx函数计算的矩阵的最小，最大值

pn：归一化后的矩阵

作用：主要用于归一化处理待分类的输入数据。

<3> postmnmx

语法： [p,t] = postmnmx(pn,minp,maxp,tn,mint,maxt)

参数：

minp，maxp：premnmx函数计算的p矩阵每行的最小值，最大值

mint，maxt：premnmx函数计算的t矩阵每行的最小值，最大值

作用：将矩阵pn，tn映射回归一化处理前的范围。postmnmx函数主要用于将神经网络的输出结果映射回归一化前的数据范围。

2. 使用Matlab实现神经网络 

使用Matlab建立前馈神经网络主要会使用到下面3个函数：

newff ：前馈网络创建函数

train：训练一个神经网络

sim ：使用网络进行仿真

 下面简要介绍这3个函数的用法。

(1) newff函数

<1>newff函数语法 

       newff函数参数列表有很多的可选参数，具体可以参考Matlab的帮助文档，这里介绍newff函数的一种简单的形式。

语法：net = newff ( A, B, {C} ,‘trainFun’)

参数：

A：一个n×2的矩阵，第i行元素为输入信号xi的最小值和最大值；

B：一个k维行向量，其元素为网络中各层节点数；

C：一个k维字符串行向量，每一分量为对应层神经元的激活函数；

trainFun ：为学习规则采用的训练算法。

<2>常用的激活函数

　　常用的激活函数有：

　　a) 线性函数 (Linear transfer function)

f(x) = x

　　该函数的字符串为’purelin’。

 

b) 对数S形转移函数( Logarithmic sigmoid transfer function )

    该函数的字符串为’logsig’。

c) 双曲正切S形函数 (Hyperbolic tangent sigmoid transfer function )

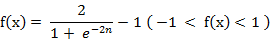
　　也就是上面所提到的双极S形函数。

 

　　该函数的字符串为’ tansig’。

　　Matlab的安装目录下的toolbox\nnet\nnet\nntransfer子目录中有所有激活函数的定义说明。

<3>常见的训练函数

    常见的训练函数有：

traingd ：梯度下降BP训练函数(Gradient descent backpropagation)

traingdx ：梯度下降自适应学习率训练函数

<4>网络配置参数

一些重要的网络配置参数如下：

net.trainparam.goal  ：神经网络训练的目标误差

net.trainparam.show   ： 显示中间结果的周期

net.trainparam.epochs 　：最大迭代次数

net.trainParam.lr    ： 学习率

(2) train函数

    网络训练学习函数。

语法：[ net, tr, Y1, E ]  = train( net, X, Y )

参数：

X：网络实际输入

Y：网络应有输出

tr：训练跟踪信息

Y1：网络实际输出

E：误差矩阵

(3) sim函数

语法：Y=sim(net,X)

参数：

net：网络

X：输入给网络的Ｋ×N矩阵，其中K为网络输入个数，N为数据样本数

Y：输出矩阵Q×N，其中Q为网络输出个数

(4) Matlab BP网络实例 

       我将Iris数据集分为2组，每组各75个样本，每组中每种花各有25个样本。其中一组作为以上程序的训练样本，另外一组作为检验样本。为了方便训练，将3类花分别编号为1，2，3 。

　　使用这些数据训练一个4输入（分别对应4个特征），3输出（分别对应该样本属于某一品种的可能性大小）的前向网络。

       Matlab程序如下：