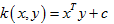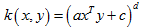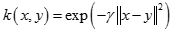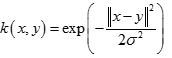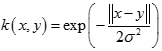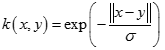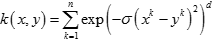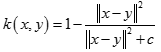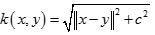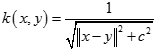高斯核KernelScale按原始内核比例缩放的RBF西格玛参数
KernelScale - 一种策略是尝试按原始内核比例缩放的RBF西格玛参数的几何序列。
以下是几种常用的核函数表示:
线性核(Linear Kernel)
多项式核(Polynomial Kernel)
径向基核函数(Radial Basis Function)
也叫高斯核(Gaussian Kernel),因为可以看成如下核函数的领一个种形式:
径向基函数是指取值仅仅依赖于特定点距离的实值函数,也就是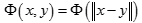
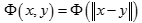
幂指数核(Exponential Kernel)
拉普拉斯核(Laplacian Kernel)
ANOVA核(ANOVA Kernel)
二次有理核(Rational Quadratic Kernel)
多元二次核(Multiquadric Kernel)
逆多元二次核(Inverse Multiquadric Kernel)
另外一个简单实用的是Sigmoid核(Sigmoid Kernel)
以上几种是比较常用的,大部分在SVM,SVM-light以及RankSVM中可用参数直接设置。还有其他一些不常用的,如小波核,贝叶斯核,可以需要通过代码自己指定。
使用fitcsvm的'OptimizeHyperparameters'名称 - 值对参数来查找最小化交叉验证损失的参数值。符合条件的参数是'BoxConstraint','KernelFunction','KernelScale','PolynomialOrder'和'Standardize'。有关示例,请参阅使用贝叶斯优化优化SVM分类器拟合。或者,您可以使用bayesopt函数,如使用bayesopt优化交叉验证的SVM分类器所示。 bayesopt功能可以更灵活地定制优化。您可以使用bayesopt函数来优化任何参数,包括使用fitcsvm函数时不适合优化的参数。
您也可以尝试根据此方案手动调整分类器的参数:
1、将数据传递给fitcsvm,并设置名称 - 值对参数'KernelScale','auto'。假设训练的SVM模型被称为SVMModel。该软件使用启发式程序来选择内核比例。启发式程序使用子采样。因此,要重现结果,请在训练分类器之前使用rng设置一个随机数种子。
2、交叉验证分类器通过传递给交叉。默认情况下,软件进行10倍交叉验证。
3、将交叉验证的SVM模型传递给kFoldLoss以估计并保留分类错误。
4、重新调整SVM分类器,但调整'KernelScale'和'BoxConstraint'名称 - 值对参数。
- BoxConstraint - 一种策略是尝试框约束参数的几何序列。例如,从1e-5到1e5取11个值10倍。增加BoxConstraint可能会减少支持向量的数量,但也可能会增加训练时间。
- KernelScale - 一种策略是尝试按原始内核比例缩放的RBF西格玛参数的几何序列。做到这一点:
a.使用点符号检索原始内核比例,例如ks:ks = SVMModel.KernelParameters.Scale。
b.用作原始内核的比例因子。例如,将ks乘以11个值1e-5到1e5,增加10倍。
选择产生最低分类错误的模型。您可能想要进一步优化您的参数以获得更好的准确性。从您的初始参数开始,并执行另一个交叉验证步骤,这次使用的因子为1.2。
用高斯内核训练SVM分类器。。
这个例子展示了如何生成一个具有高斯核函数的非线性分类器。首先,在单元圆盘内部生成一类二维点,然后在半径为1到半径2的圆环中生成另一类点。然后,根据具有高斯径向基函数内核的数据生成分类器。由于模型是圆对称的,因此默认的线性分类器显然不适合这个问题。将框约束参数设置为Inf以进行严格分类,这意味着不存在错误分类的训练点。其他内核函数可能不适用于这种严格的框约束,因为它们可能无法提供严格的分类。即使rbf分类器可以分离类,结果也可能会过度训练。
生成均匀分布在单位磁盘上的100个点。为此,生成半径r作为均匀随机变量的平方根,在(0,)中均匀生成一个角度t,并将该点置于(rcos(t),rsin(t))。