Ansys杆单元LINK180模拟仅受拉或仅受压大变形非线性计算算例

1、模型介绍

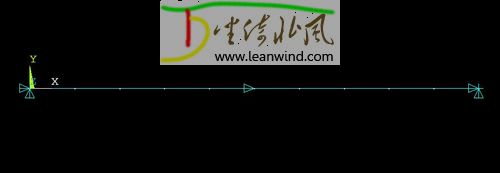
模型如下图所示，杆的两端固定，中间节点施加一个沿杆轴线方向的强制位移l = 5mm。杆长度L = 100mm，截面积S=100mm²，弹性模量E=10MPa。

假定杆为仅受拉杆件（如绳索等），求解杆两端的约束反力并与理论值进行对比。

2、Ansys有限元建模

在Ansys中建立如上图所示有限元模型，网格大小设置为10mm，单元设置为LINK180，并设置材料属性。由于LINK180单元的第3个实常数TENSKEY仅可在Ansys中通过命令方式定义，因此通过如下命令定义LINK180的单元实常数：

R,1,100,0,1

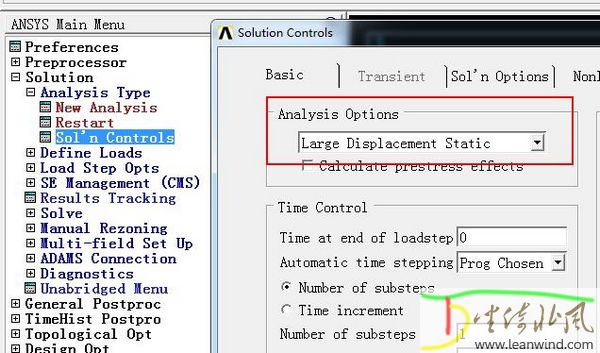
通过菜单Solution – Analysis Type – Sol’n Controls，在Basic选项卡中将Analysis Options设置为Large Displacement Static，打开非线性大变形选项。

3、有限元求解

对以上模型进行求解，列出模型的支反力如下：

NODE      FX

1        -86.646

6         86.646

11        0.0000

下面是杆的变形云图。

4、理论计算

节点处的支反力可由下式进行计算：

F=0.5L*S*E*ln（1+l/（0.5L））/（0.5L+l）

将数值带入以上公式求得左侧支点处的支反力为：-86.646，与有限元求解结果相同。

5、结论

Ansys的LINK180杆单元是一种理想的模型，仅需一个单元即可获得精确解，十分适合模拟杆件结构。若要模拟仅受压（如轴承等）或仅受拉（如绳索等）结构则需定义LINK180单元的第三个实常数（仅可通过命令方式定义）：TENSKEY = -1（仅受压）或TENSKEY = 1（仅受拉）。且必须打开大变形选项，采用非线性计算。值得注意的是，大变形分析将考虑截面变形引起的刚度变化，而小变形计算将杆考虑为固定刚度。